二叉树
二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只有左子节点,有的节点只有右子节点。
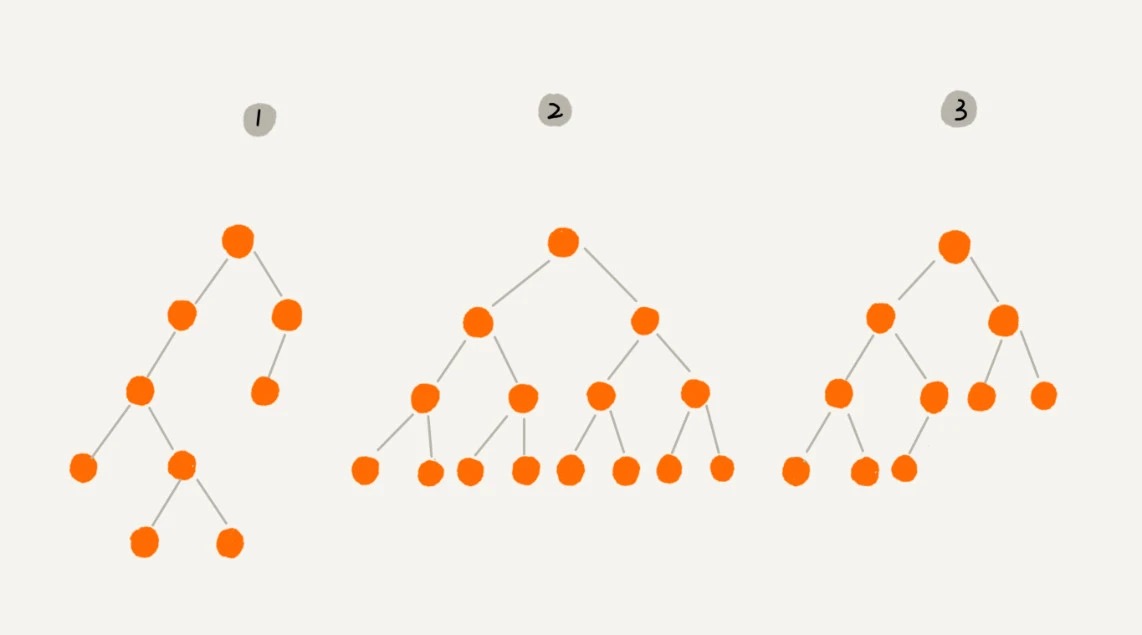
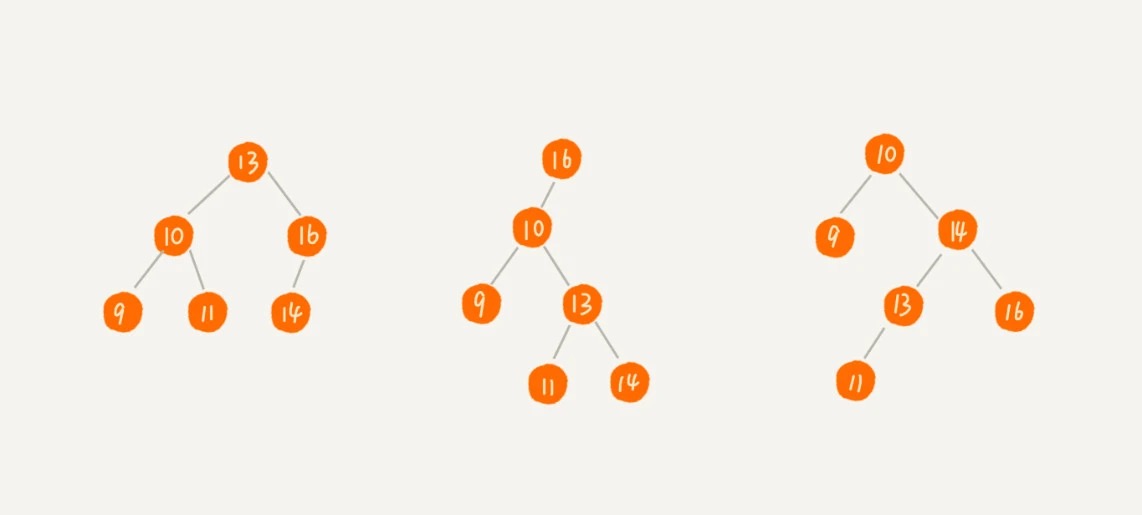
编号 2 的二叉树中,叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树就叫做 满二叉树。
编号 3 的二叉树中,叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫做 完全二叉树。
如何表示(或者存储)一棵二叉树?#
一种是基于指针或者引用的二叉 链式存储法,一种是基于数组的 顺序存储法。
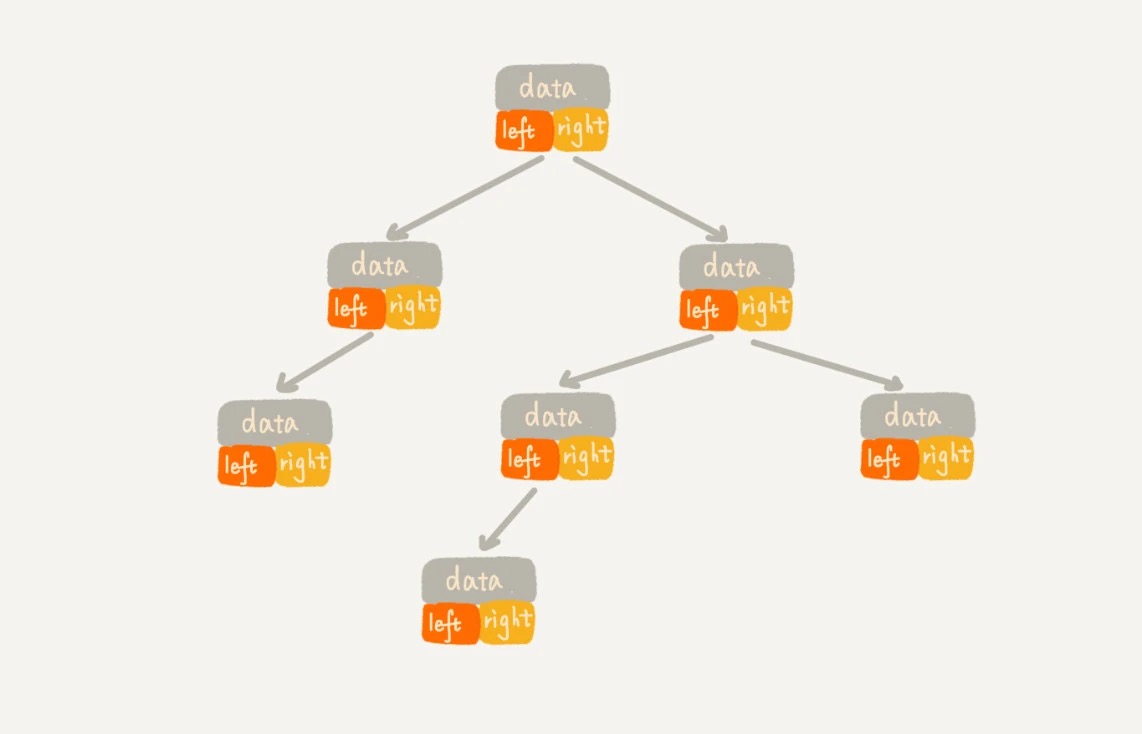
链式存储法。从图中你应该可以很清楚地看到,每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针。我们只要拎住根节点,就可以通过左右子节点的指针,把整棵树都串起来。这种存储方式我们比较常用。大部分二叉树代码都是通过这种结构来实现的。
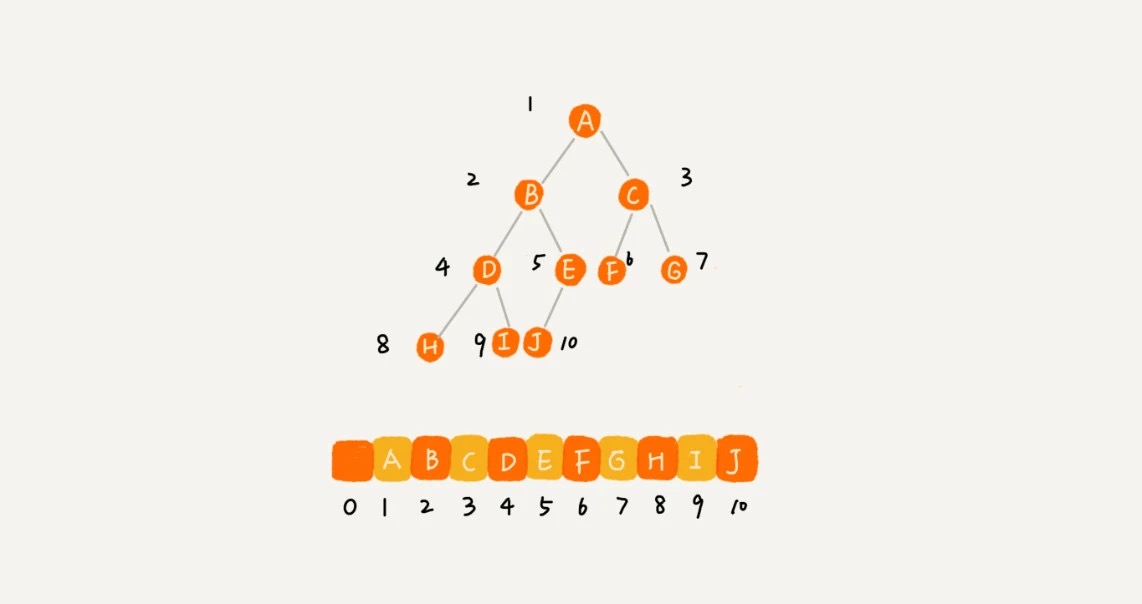
基于数组的顺序存储法。我们把根节点存储在下标 i = 1 的位置,那左子节点存储在下标 2 * i = 2 的位置,右子节点存储在 2 * i + 1 = 3 的位置。以此类推,B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置,右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。
刚刚举的例子是一棵完全二叉树,所以仅仅“浪费”了一个下标为 0 的存储位置。如果是非完全二叉树,其实会浪费比较多的数组存储空间。可以看举的下面这个例子
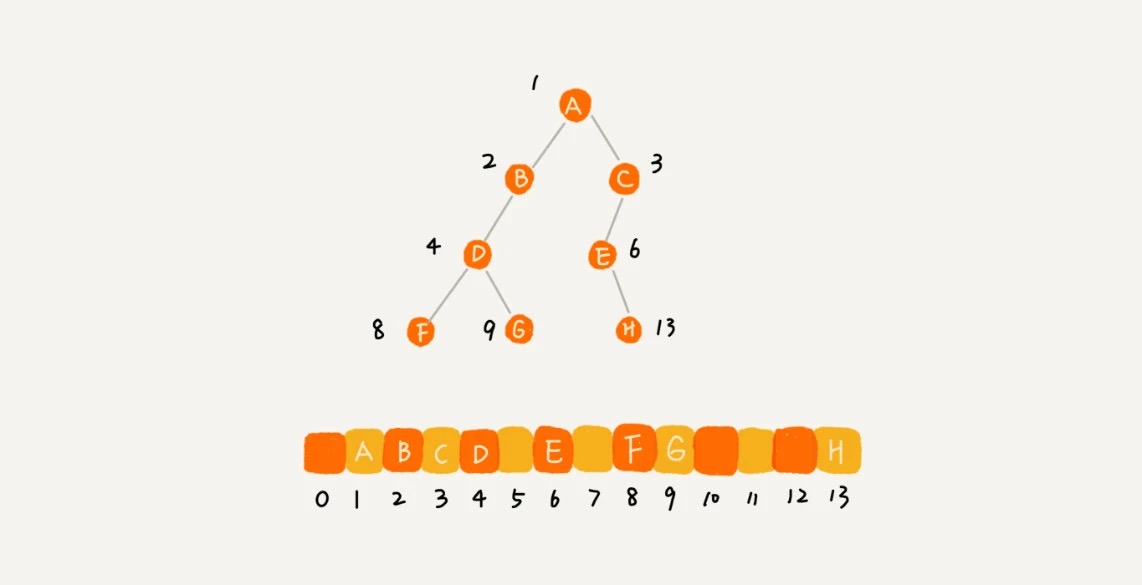
所以,如果某棵二叉树是一棵完全二叉树,那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样,要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因,也是为什么完全二叉树要求最后一层的子节点都靠左的原因。
二叉树的遍历#
经典的方法有三种,前序遍历、中序遍历和后序遍历:
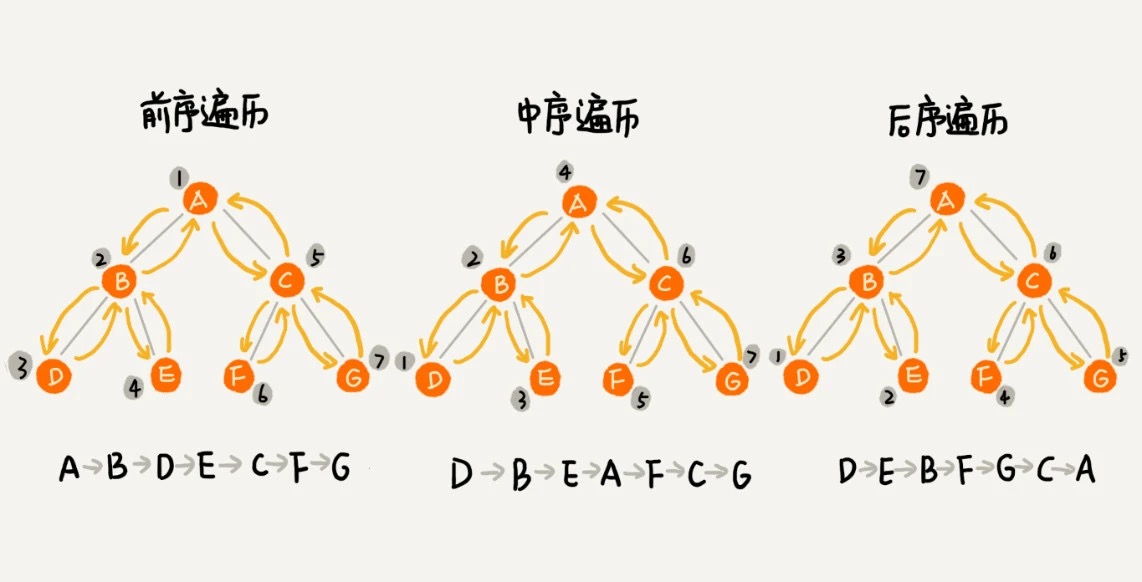
- 前序遍历:对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
- 中序遍历:对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
- 后序遍历:对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。 实际上就是遍历本身节点的顺序问题。
// 先序function preOrder(root) { if (root == null) return; console.log(root.value); preOrder(root.left); preOrder(root.right);}
// 中序function inOrder(root) { if (root == null) return; inOrder(root.left); console.log(root.value); inOrder(root.right);}
// 后序function postOrder(root) { if (root == null) return; postOrder(root.left); postOrder(root.right); console.log(root.value);}二叉查找树#
也叫二叉搜索树,二叉查找树最大的特点就是,支持动态数据集合的快速插入、删除、查找操作。 二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
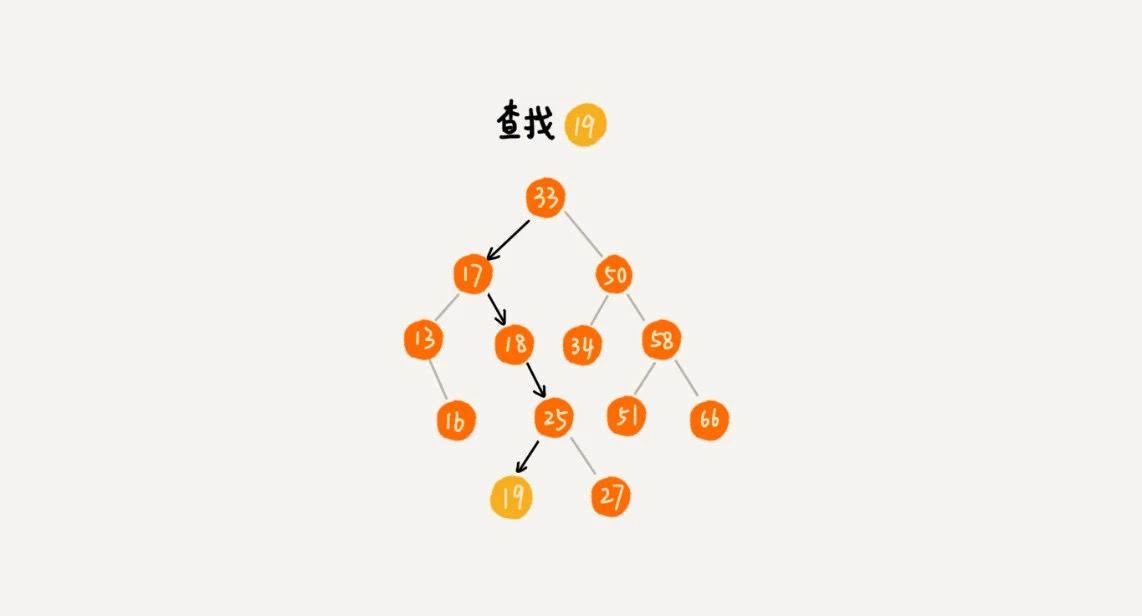
1. 二叉查找树的查找操作#
我们先取根节点,如果它等于我们要查找的数据,那就返回。如果要查找的数据比根节点的值小,那就在左子树中递归查找;如果要查找的数据比根节点的值大,那就在右子树中递归查找。
function TreeNode(val) { this.val = val; this.left = this.right = null;}function searchBST(root, val) { while (root !== null && val !== root.val) { root = val < root.val ? root.left : root.right; } return root;}2. 二叉查找树的插入操作#
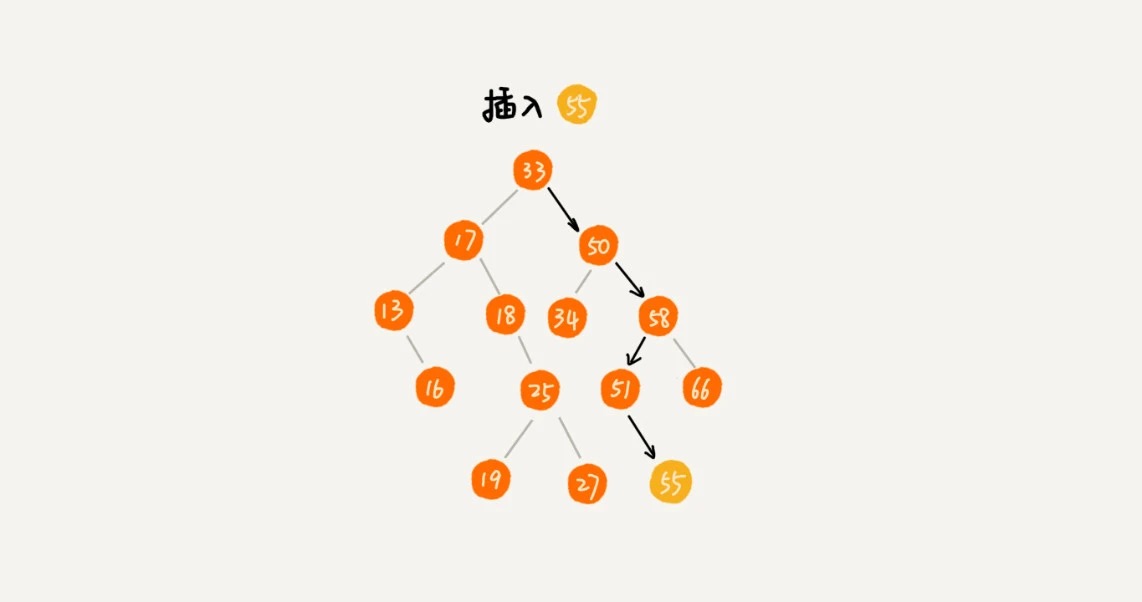
如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。同理,如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
function TreeNode(val) { this.val = val; this.left = this.right = null;}function insertBST(root, val) { if (root === null) { root = new TreeNode(val); return root; } while (root != null) { if (val > root.val) { if (root.right == null) { root.right = new TreeNode(val); return root; } root = root.right; } else { if (root.left == null) { root.left = new TreeNode(val); return root; } root = root.left; } }}3. 二叉查找树的删除操作#
针对要删除节点的子节点个数的不同,我们需要分三种情况来处理。
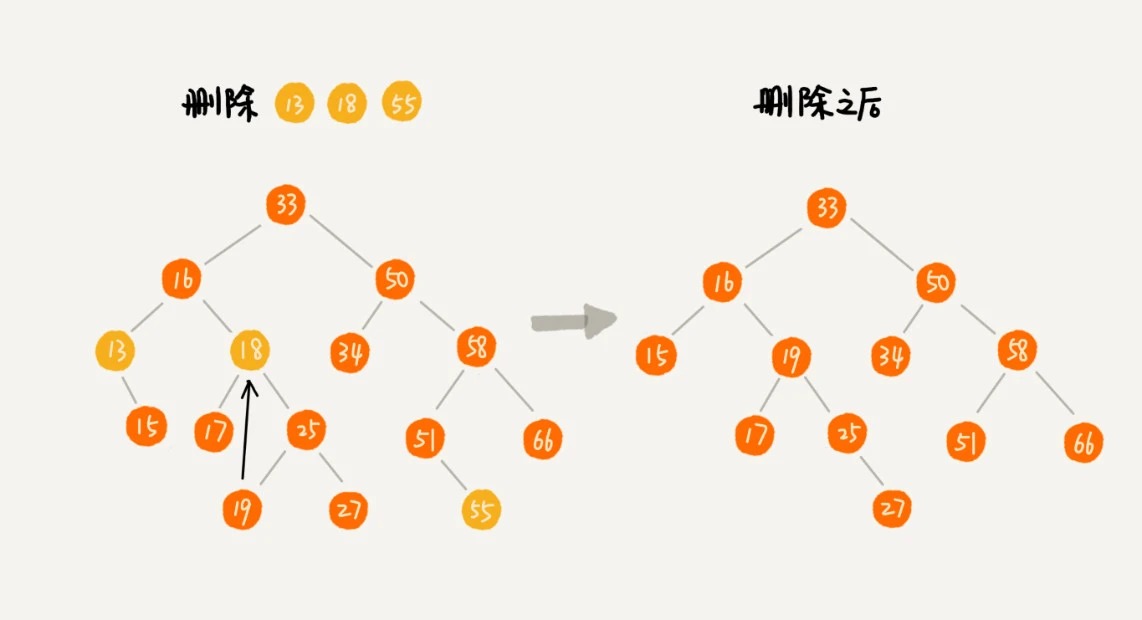
- 如果要删除的节点没有子节点,我们只需要直接将父节点中,指向要删除节点的指针置为 null。比如图中的删除节点 55。
- 如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。
- 如果要删除的节点有两个子节点,这就比较复杂了。我们需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。
function TreeNode(val) { this.val = val; this.left = this.right = null;}function deleteNode(root, key) { if (!root) return null; if (root.val > key) { root.left = deleteNode(root.left, key); return root; } if (root.val < key) { root.right = deleteNode(root.right, key); return root; } if (root.val === key) { if (!root.left && !root.right) { return null; } if (!root.right) { return root.left; } if (!root.left) { return root.right; } let p = root.right; while (p.left) { p = p.left; } root.right = deleteNode(root.right, p.val); p.right = root.right; p.left = root.left; return p; }};平衡二叉查找树#
平衡二叉树:二叉树中任意一个节点的左右子树的高度相差不能大于 1。从这个定义来看,完全二叉树、满二叉树其实都是平衡二叉树,但是非完全二叉树也有可能是平衡二叉树。
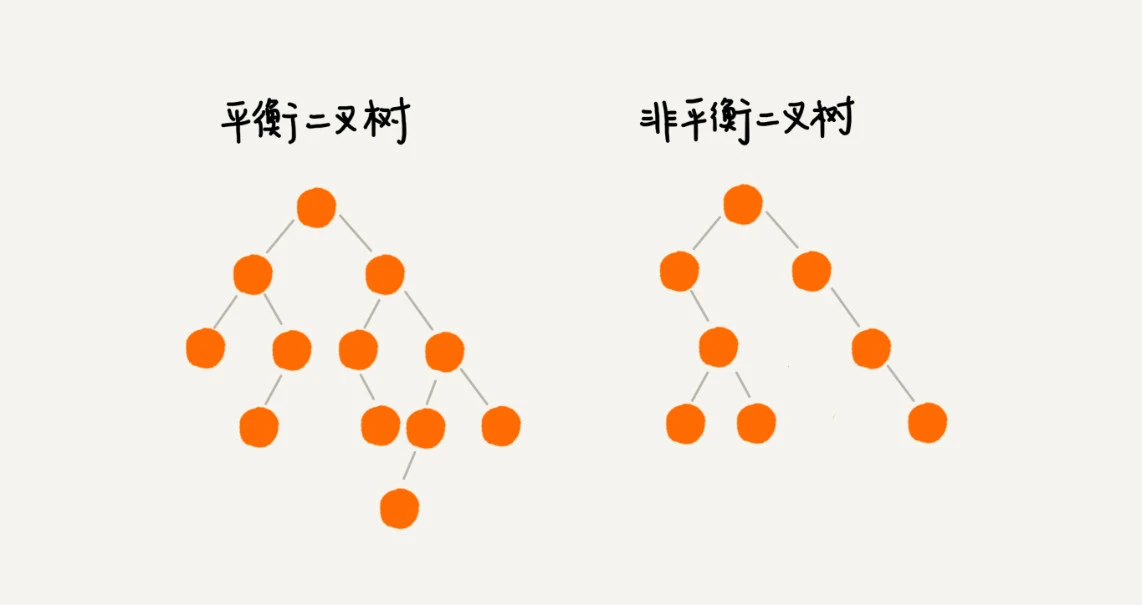
平衡二叉查找树不仅满足上面平衡二叉树的定义,还满足二叉查找树的特点。最先被发明的平衡二叉查找树是AVL树,它严格符合平衡二叉查找树的定义,即任何节点的左右子树高度相差不超过 1,是一种高度平衡的二叉查找树。 发明平衡二叉查找树这类数据结构的初衷是,解决普通二叉查找树在频繁的插入、删除等动态更新的情况下,出现时间复杂度退化的问题。 所以,平衡二叉查找树中“平衡”的意思,其实就是让整棵树左右看起来比较“对称”、比较“平衡”,不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些,相应的插入、删除、查找等操作的效率高一些。
红黑树#
红黑树的英文是“Red-Black Tree”,简称 R-B Tree。它是一种不严格的平衡二叉查找树。红黑树中的节点,一类被标记为黑色,一类被标记为红色。除此之外,一棵红黑树还需要满足这样几个要求:
- 根节点是黑色的
- 每个叶子节点都是黑色的空节点,也就是说,叶子节点不存储数据
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点