Binary tree, as the name suggests, each node can have at most two "branches", which are the left child node and the right child node. However, a binary tree does not require each node to have two child nodes. Some nodes only have a left child node, and some nodes only have a right child node.
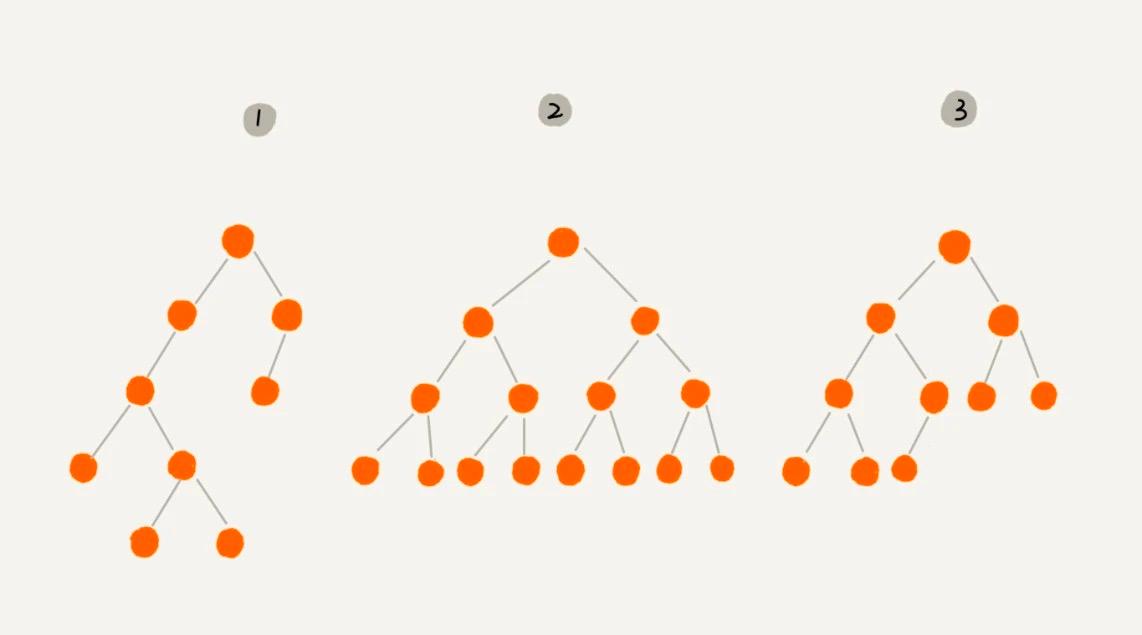
In the binary tree with number 2, all the leaf nodes are at the bottom. In addition to the leaf nodes, each node has both a left and a right child node. This type of binary tree is called a full binary tree.
In the binary tree with number 3, all the leaf nodes are at the bottom two levels. The leaf nodes in the last level are arranged from left to right, and except for the last level, the number of nodes in each level should be the maximum. This type of binary tree is called a complete binary tree.
How to represent (or store) a binary tree?#
One way is to use the pointer-based or reference-based binary tree storage method, and the other way is to use the array-based sequential storage method.
Pointer-based storage method. From the diagram, you should be able to see clearly that each node has three fields, one stores data, and the other two are pointers to the left and right child nodes. As long as we hold the root node, we can link the entire tree through the pointers of the left and right child nodes. This storage method is commonly used. Most binary tree code is implemented using this structure.
Array-based sequential storage method. We store the root node at index i = 1, the left child node at index 2 * i = 2, and the right child node at index 2 * i + 1 = 3. Similarly, the left child node of node B is stored at index 2 * i = 2 * 2 = 4, and the right child node is stored at index 2 * i + 1 = 2 * 2 + 1 = 5.
The example just mentioned is a complete binary tree, so it only "wastes" one storage position with index 0. If it is not a complete binary tree, it will actually waste more array storage space. You can see the example below.
Therefore, if a binary tree is a complete binary tree, using an array to store it is undoubtedly the most memory-saving method. Because the array storage method does not require storing additional pointers to the left and right child nodes like the pointer-based storage method. This is also the reason why complete binary trees are singled out and why complete binary trees require the last level of child nodes to be arranged from left to right.
Traversal of binary trees#
There are three classic methods: pre-order traversal, in-order traversal, and post-order traversal:
- Pre-order traversal: For any node in the tree, first print the node, then print its left subtree, and finally print its right subtree.
- In-order traversal: For any node in the tree, first print its left subtree, then print the node itself, and finally print its right subtree.
- Post-order traversal: For any node in the tree, first print its left subtree, then print its right subtree, and finally print the node itself.
In fact, it is the order in which the nodes themselves are traversed.
// Pre-order
function preOrder(root) {
if (root == null) return;
console.log(root.value);
preOrder(root.left);
preOrder(root.right);
}
// In-order
function inOrder(root) {
if (root == null) return;
inOrder(root.left);
console.log(root.value);
inOrder(root.right);
}
// Post-order
function postOrder(root) {
if (root == null) return;
postOrder(root.left);
postOrder(root.right);
console.log(root.value);
}
Binary Search Tree#
Also known as a binary search tree, the biggest feature of a binary search tree is that it supports fast insertion, deletion, and search operations for dynamic data sets. A binary search tree requires that for any node in the tree, the value of each node in its left subtree must be less than the value of this node, and the value of each node in its right subtree must be greater than the value of this node.
1. Search operation of binary search tree#
First, take the root node. If it is equal to the data we are looking for, return it. If the data to be searched is smaller than the value of the root node, recursively search in the left subtree; if the data to be searched is larger than the value of the root node, recursively search in the right subtree.
2. Insert operation of binary search tree#
If the data to be inserted is larger than the value of the node and the right subtree of the node is empty, insert the new data directly into the position of the right child node; if it is not empty, recursively traverse the right subtree to find the insertion position. Similarly, if the data to be inserted is smaller than the value of the node and the left subtree of the node is empty, insert the new data into the position of the left child node; if it is not empty, recursively traverse the left subtree to find the insertion position.
3. Delete operation of binary search tree#
Depending on the number of child nodes of the node to be deleted, we need to handle three cases.
- If the node to be deleted has no child nodes, we only need to set the pointer in the parent node that points to the node to be deleted to null. For example, deleting node 55 in the diagram.
- If the node to be deleted has only one child node (either a left child node or a right child node), we only need to update the pointer in the parent node that points to the node to be deleted to point to the child node of the node to be deleted. For example, deleting node 13 in the diagram.
- If the node to be deleted has two child nodes, it becomes more complicated. We need to find the minimum node in the right subtree of this node, replace it with the node to be deleted, and then delete this minimum node. Because the minimum node definitely does not have a left child node (if it has a left child node, it is not the minimum node), we can use the above two rules to delete this minimum node.
Balanced Binary Search Tree#
A balanced binary tree: For any node in the binary tree, the height difference between its left and right subtrees cannot exceed 1. From this definition, complete binary trees and full binary trees are actually balanced binary trees, but non-complete binary trees may also be balanced binary trees.
The original intention of inventing balanced binary search trees and similar data structures is to solve the problem of time complexity degradation in ordinary binary search trees under frequent insertion, deletion, and other dynamic update operations.
Therefore, the "balance" in a balanced binary search tree actually means making the entire tree look relatively "symmetrical" and "balanced" from left to right, without having a situation where the left subtree is very high and the right subtree is very short. This can make the height of the entire tree relatively low, and the efficiency of corresponding operations such as insertion, deletion, and search will be higher.
Red-Black Tree#
The English name of the red-black tree is "Red-Black Tree", abbreviated as R-B Tree. It is a type of non-strict balanced binary search tree. In a red-black tree, nodes are marked as either black or red. In addition, a red-black tree needs to satisfy the following requirements:
- The root node is black.
- Every leaf node is a black empty node, which means that the leaf nodes do not store data.
- No two adjacent nodes can both be red, which means that red nodes are separated by black nodes.
- For every node, every path from the node to its descendant leaf nodes contains the same number of black nodes.